Welcome to AP Statistics Unit 1 Practice, a comprehensive guide designed to help you master the fundamentals of exploratory data analysis and sampling. Join us as we delve into the fascinating world of statistics, where we’ll uncover the secrets of data exploration and sampling techniques.

This guide will equip you with the knowledge and skills necessary to understand the distribution of data, construct confidence intervals, test hypotheses, and compare population means. Whether you’re a seasoned statistician or just starting your journey, this practice guide is your passport to statistical success.

AP Statistics Unit 1 Practice: Exploratory Analysis of Univariate Data

Exploratory data analysis (EDA) is a crucial step in AP Statistics Unit 1. It involves exploring and understanding the characteristics of a dataset before performing any statistical analysis. EDA helps identify patterns, trends, and potential outliers that may not be evident from a cursory examination.

Graphical Methods for Univariate Data Exploration

Graphical methods are powerful tools for visualizing the distribution of univariate data. These methods include:

• -*Stem-and-leaf plots

  Display data values as stems and leaves, providing a visual representation of the data’s distribution.

-*Box plots

Show the median, quartiles, and potential outliers, summarizing the data’s central tendency and spread.

-*Histograms

Divide the data into bins and display the frequency of data points in each bin, revealing the shape of the distribution.

Numerical Methods for Univariate Data Exploration, Ap statistics unit 1 practice

Numerical methods provide quantitative measures to describe the data’s characteristics. These methods include:

• -*Measures of central tendency

  Mean, median, and mode describe the typical value in the dataset.

-*Measures of spread

Range, variance, and standard deviation measure the variability or dispersion of the data.

-*Skewness and kurtosis

Describe the asymmetry and peakedness of the distribution, respectively.

Advantages and Limitations of EDA Techniques

Advantages:

• -*Identify patterns and trends

  EDA helps uncover relationships and patterns within the data.

-*Detect outliers

EDA can identify unusual data points that may indicate errors or influential observations.

-*Inform statistical analysis

EDA provides insights that guide subsequent statistical analysis, such as hypothesis testing and modeling.

Limitations:

• -*Subjectivity

  Graphical methods can be subjective in interpreting patterns and trends.

-*Small sample size

EDA may not provide reliable insights for datasets with a small sample size.

-*High dimensionality

EDA becomes challenging for datasets with many variables.

Sampling and Sampling Distributions

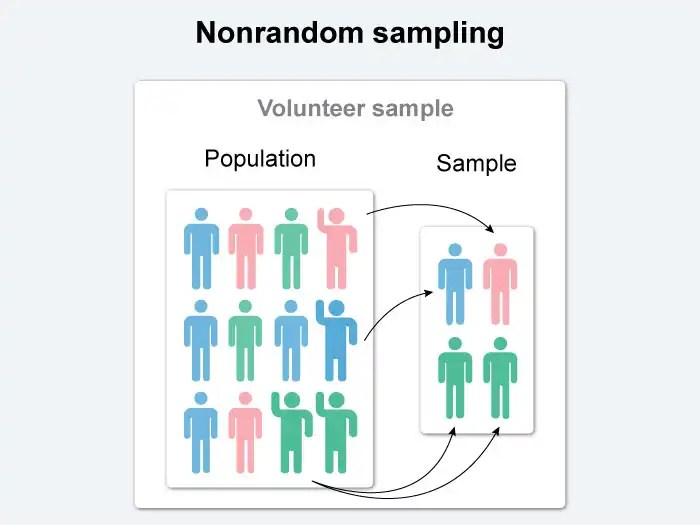
Sampling is the process of selecting a subset of a population to make inferences about the entire population. Different sampling methods exist, each with its own advantages and disadvantages.

Types of Sampling Methods

• Simple random sampling:Each member of the population has an equal chance of being selected.
• Systematic sampling:Members are selected at regular intervals from a list or roster.
• Stratified sampling:The population is divided into strata, and then a random sample is taken from each stratum.
• Cluster sampling:The population is divided into clusters, and then a random sample of clusters is selected.
• Convenience sampling:Members are selected based on their accessibility or convenience.

Sampling Distributions

A sampling distribution is the distribution of all possible sample means that could be obtained from all possible samples of a given size from a population. The properties of a sampling distribution include its shape, center, and spread.

Central Limit Theorem

The Central Limit Theorem states that the sampling distribution of sample means will be approximately normal, regardless of the shape of the population distribution, provided the sample size is sufficiently large (typically n ≥ 30).

This theorem is crucial in statistical inference, as it allows us to make inferences about the population mean based on the sample mean, even if the population distribution is unknown.

Confidence Intervals for a Population Mean

In statistics, a confidence interval is a range of values that is likely to contain the true population mean. It is calculated using a sample statistic, such as the sample mean, and a margin of error.

Formula for Confidence Intervals

The formula for constructing a confidence interval for a population mean is:

CI = x̄ ± z* (σ/√n)

• x̄ is the sample mean
• z is the z-score corresponding to the desired confidence level
• σ is the population standard deviation
• n is the sample size

Factors Affecting the Width of a Confidence Interval

The width of a confidence interval is affected by three factors:

• Sample size:The larger the sample size, the narrower the confidence interval.
• Population standard deviation:The larger the population standard deviation, the wider the confidence interval.
• Confidence level:The higher the confidence level, the wider the confidence interval.

Hypothesis Testing for a Population Mean

Hypothesis testing is a statistical method used to determine whether a claim about a population parameter is supported by the available evidence. The steps involved in hypothesis testing are as follows:

• State the null hypothesis (H0) and the alternative hypothesis (Ha).
• Set the significance level (alpha).
• Calculate the test statistic.
• Determine the p-value.
• Make a decision about the null hypothesis.

The test statistic is a measure of the difference between the sample mean and the hypothesized population mean. The p-value is the probability of obtaining a test statistic as extreme as or more extreme than the one calculated, assuming that the null hypothesis is true.There

If you’re prepping for AP Statistics Unit 1 practice, you might want to take a break and read “To Kill a Mockingbird” by Harper Lee. Lennie’s story will provide you with valuable insights into human nature, which can be helpful when analyzing statistical data and making inferences about the population.

Don’t forget to return to your AP Statistics Unit 1 practice afterward!

are two types of errors that can occur in hypothesis testing:

1. Type I error

Rejecting the null hypothesis when it is true.

2. Type II error

Failing to reject the null hypothesis when it is false.The significance level is the probability of making a Type I error. The power of a hypothesis test is the probability of rejecting the null hypothesis when it is false.

Comparing Two Population Means

Comparing two population means is a statistical technique used to determine if there is a significant difference between the means of two populations. It is widely used in various fields, such as healthcare, education, and social sciences, to draw inferences about population characteristics.

Methods for Comparing Two Population Means

There are two primary methods for comparing two population means:

1. Independent Samples t-test:Used when the samples from the two populations are independent, meaning that the selection of one sample does not affect the selection of the other sample.
2. Paired Samples t-test:Used when the samples are paired, meaning that each subject or observation in one sample has a corresponding subject or observation in the other sample.

Assumptions for Comparing Two Population Means

To ensure the validity of the comparison, certain assumptions must be met:

• The samples must be random and representative of the respective populations.
• The populations should be normally distributed or have a large enough sample size to satisfy the Central Limit Theorem.
• The variances of the two populations should be equal (homogeneity of variances).

Test Statistic and p-value Calculation

The test statistic for both the independent and paired samples t-tests is calculated as follows:

t = (x̄₁

• x̄ ₂) / (s _p
• √(1/n ₁+ 1/n ₂))

where:* x̄ ₁and x̄ ₂are the sample means of the two populations

s_pis the pooled standard deviation, calculated as

s _p= √((n ₁-1)*s ₁²+ (n ₂-1)*s ₂²) / (n ₁+ n ₂

• 2))
• n ₁and n ₂are the sample sizes of the two populations

The p-value is calculated using a t-distribution with degrees of freedom equal to the smaller of (n ₁-1) and (n ₂-1).

Answers to Common Questions

What is the purpose of exploratory data analysis?

Exploratory data analysis helps us understand the distribution of data, identify patterns and trends, and generate hypotheses for further investigation.

What is the Central Limit Theorem?

The Central Limit Theorem states that the distribution of sample means approaches a normal distribution as the sample size increases, regardless of the shape of the population distribution.

What is the difference between a confidence interval and a hypothesis test?

A confidence interval estimates the range of values within which the true population parameter is likely to fall, while a hypothesis test determines whether there is sufficient evidence to reject a null hypothesis.